Vi è piaciuta galleria Spada? quali sono le vostre impressioni? Rifletteteci: la prossima volta vorrei foste voi a dirmi a cosa vi fa pensare il connubio “arte-matematica” (NON è ammessa la risposta: “sono due materie scolastiche”, come qualcuno mi disse, riguardo la matematica, nel primo incontro!! Studenti avvisati….)

Iniziamo con un contributo della prof. ssa Catastini  (par. 7 del contributo “Dalla geometria della visione alla trasformazione prospettica”,  in Matematica e Arte. Forme del pensiero artistico, a cura di Laura Catastini e Franco Ghione).

Per favore riportate le copie che vi ho lasciato! mi sono sbagliata, è meglio se le diamo agli assenti, poi in caso provvediamo a farne copie per tutti. Posso provare a fare le foto e caricarle qui…..

il risultato è pessimo!!!!!!!!!!! eccole 

Ciò che abbiamo letto in classe è un paragrafo sul cosiddetto “punto all’infinito” di una retta, o meglio di un fascio di rette parallele. Come sappiamo, rette parallele NON hanno punti in comune.. cos’è allora questo “punto” (che, essendo “all’infinito”, non vediamo concretamente) comune a rette parallele? O, semplificando ancora di più, che cos’è che tutte le rette parallele tra di loro hanno in comune?

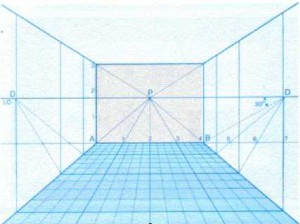
Come ha giustamente detto Francesca (e per questo si è meritata un cioccolatino post-epifania): la DIREZIONE! Ci siamo quindi convinti (o almeno spero) che il punto di fuga di un quadro, ad esempio, è il punto all’infinito di tutte le linee di profondità (cioè delle rette perpendicolari al piano del quadro).

Volendo semplificare ancora di più (ma solo per gli assenti! invito invece coloro che erano presenti a finire di leggere il paragrafo, dove si parla dell’esperienza in classe col prospettimetro) e anticipando uno degli argomenti che faremo (spero anche con la proiezione di Flatlandia) cioè il concetto di dimensione, possiamo dire che il punto di fuga, o il punto all’infinito delle rette di profondità, è l’artificio mediante il quale si rende, su una superficie bidimensionale (cioè “piatta” nel senso che si estende solo in lunghezza e larghezza), quale un foglio un quadro o una parete, la terza dimensione, ovvero proprio la profondità.

Proseguiamo leggendo qualche verso del De rerum natura di Lucrezio (libro IV, vv 426-431):

Un portico benché abbia profilo costante,
e appoggi completamente su uguali colonne,
se si vede da una parte finale in tutta la sua lunghezza,
poco a poco si stringe nella punta di un cono sottile
congiungendo tetto e suolo, tutto ciò che sta a destra e a sinistra,
fino a terminare nella punta oscura di un cono.

… ed ecco la versione originale!! Contenti?!

Porticus aequali quamvis est denique ductu    

stansque in perpetuum paribus suffulta columnis,

longa tamen parte ab summa cum tota videtur,  

paulatim trahit angusti fastigia coni,  

tecta solo iungens atque omnia dextera laevis

donec in obscurum coni conduxit acumen.

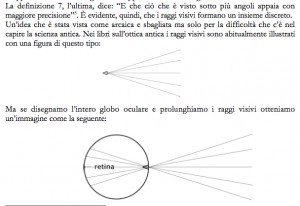
Infine abbiamo osservato le immagini proposte nell’articolo In obscurum coni conduxit acumen  (che poi è l’ultimo verso) sempre di Laura Catastini e Franco Ghione.

Ci siamo poi chiesti: com’è possibile che una “scienza” (nel senso di “qualcosa che si sa”,  da scĭo, scis, scii, scitum, scīre) vada perduta? Cioè che i pittori, fino al Rinascimento, in cui nasce un nuovo interesse per gli autori classici greci e latini, non sapessero come si fa una resa prospettica, e che quindi si affidassero una rappresentazione prospettica “intuitiva” (e sbagliata, poichè non vi era un punto di fuga, che esiste ed è unico)? Questo ci ha portati a riflettere su cosa sia la cultura, su come si costruisce e si tramanda il sapere, e sui rischi dei periodi di buio della ragione (p. es. il Medioevo, ma non è che di ‘sti tempi ce la passiamo tanto meglio.. e se ci scordassimo di come si scrive? se iniziassimo tt @ scrvr prpr cm i bimbim**kia??!?! 😛 😉 XD !!1!!!11!!!  LOL)

Con questa lezione concludiamo la prospettiva e la teoria della visione (per una trattazione completa si veda il libro “Le geometrie della visione. Scienza, arte didattica” di L. Catastini e F. Ghione, 2004 Springer); come vi ho detto vorrei inserire nel programma un argomento che inizialmente non c’era: numeri di Fibonacci, sezione aurea e spirali (e conseguentemente anticiperemo la parte sui frattali, anche perchè ho paura che, se la lascio a marzo a fine corso, poi non trovo più i broccoli da farvi vedere!! hehe, poi vi spiego.. )

Ho cambiato di nuovo idea! Il corso proseguirà con

• Dimensione: la quarta dimensione, proiezione di Flatlandia (se trovo il dvd), politopi (accenni).
• Simmetrie: poligoni e poliedri (platonici), il concetto di simmetria (piana), tassellazioni, fiocchi di neve (e dna), architettura, decorazioni di stuoie africane.
• Sezione aurea, Fibonacci e spirali: sezione/rettangolo/triangolo/rapporto aurei e spirale logaritmica, architettura, il concetto di successione (e induzione), i numeri di Fibonacci, ancora la spirale logaritmica, la fillotassi (e un po’ di frattali)
• Lo specchio magico di M. C. Escher
• Musica

(Ma devo capire quanto tempo mi resta per gli ultimi due punti)

Con vostra somma gioia, la scorsa volta abbiamo letto le premesse dell’Ottica direttamente in greco. Vi ho anticipato in maniera un po’ affrettata molte delle costruzioni e delle regole grammaticali e sintattiche che vedrete nel corso degli studi (spero di non avervi spaventati!…).

Abbiamo visto le parole per: linea retta, angolo, raggio, etc.. e inoltre scoperto che il verbo “prospipto”, da cui prospettiva, vuol dire……… (vedi in alto a dx nella foto)

[avete cercato autonomamente la parola “schema”?  ricordate, è col chi e con l’eta!]

______________________

Abbiamo poi letto (in traduzione) le proposizioni che prescrivono come realizzare una prospettiva centrale:

Proposizione 6: Intervalli paralleli visti a distanza appaiono disegualmente larghi

(e quindi vediamo convergere linee parallele che si allontanano da noi, come ad esempio due binari, o le pareti di un corridoio infinitamente lungo..)

Proposizione 10: Dei piani posti sotto l’occhio, quelli lontano appaiono più alti

Proposizione 11: Dei piani posti sopra l’occhio, quelli lontani appaiono più bassi

Proposizione 12: Delle grandezze che hanno lunghezza in avanti, quelle a destra sembrano deviare verso sinistra, quelle a sinistra verso destra

Proposizione 13: Delle grandezze uguali e poste sotto lo stesso occhio, quelle lontane appaiono più alte

Proposizione 14: Delle grandezze uguali e poste sopra l’occhio quelle lontano appaiono più basse

Abbiamo verificato poi, con le file di banchi e gli angoli sotto cui vedevamo le loro estremità, che le proposizioni sono tutte vere (se interpretate correttamente! qualcuno nel provare a fare un controesempio nel caso della proposizione 10, non ha tenuto conto dell’ipotesi che i piani in considerazione siano sotto l’occhio).

Ciò che dovreste avere in mente, è uno schema (ancora: andatevi a cercare il significato sul dizionario di greco!) tipo questo, che l’altra volta non ho avuto il tempo di mostrarvi

_______________________________

Vi ho inoltre fatto notare che la Proposizione 5

è vera solo nel caso in cui ci si ponga frontalmente, rispetto a tali grandezze: con una penna abbiamo verificato che se il punto di vista è “sufficientemente laterale”, l’angolo sotto cui la vediamo è più piccolo di quello sotto cui vediamo una penna più lontana.

L’Ottica di Euclide contiene 62 proposizioni. Esse sono precedute da delle “definizioni” (hòroi) che però sono ben diverse da quelle degli Elementi, le quali fissano gli oggetti di cui si parla (“dicasi punto / retta / cerchio” etc..). Le “definizioni” dell’Ottica sono piuttosto delle “premesse” su come appunto si imposta lo studio della visione secondo il matematico ellenistico. Vediamole.

Premesse:

1. Sia posto che le linee rette condotte fuori dall’occhio si muovano per un intervallo di grandi grandezze
   [in realtà, la giusta traduzione è probabilmente “si estendano per distanze (angolari) reciproche molto diverse“, vedi Silvio M. Medaglia-Lucio Russo, Sulla prima “definizione” dell’Ottica di Euclide , in “Bollettino dei Classici”, Accademia dei Lincei, 16 (1995), pp. 41-54, ndr]
2. E che la figura compresa dai raggi visivi sia un cono che ha il vertice nell’occhio e la base sui contorni delle cose viste.
3. E che siano viste quelle cose sulle quali incidono i raggi visivi, e non sia visto ciò su cui non incidono i raggi visivi.
4. E che ciò che è visto sotto un angolo maggiore appaia maggiore, quello sotto un angolo minore appaia minore, e uguale ciò che è visto sotto angoli uguali.
5. E che ciò che è visto da raggi più alti appaia più alto, quello da raggi più bassi più basso.
6. E che similmente ciò che è visto da raggi più a destra appaia più a destra, quello da raggi più a  sinistra più a sinistra
7. E che ciò che è visto sotto più angoli appaia con maggiore precisione.

(Da Tutte le opere, Euclide; introduzione, traduzione, note e apparati di Fabio Acerbi. Milano, Bompiani il pensiero occidentale, 2007.)

_____________________________________________________

Abbiamo visto il testo originale greco, riconoscendo alcuni termini, quali “linee”, “occhio”, “vista”, “condurre”, “cono”, “angolo”, “raggio”…

Vi ho poi fatto riflettere sul fatto che al tempo dei greci non vi fosse una distinzione tra il ruolo del matematico, del fisico o dell’ingegnere: la matematica (ciò che si può studiare, ciò che si può apprendere) comprendeva tantissime materie di studio (tutte quelle in cui, da un problema più o meno concreto, si cercava di ricavare una legge sempre valida, dati certi presupposti). Insomma non esistevano solo “teoremi” di aritmetica o di geometria, ma anche di astronomia, idrostatica, musica, ottica, meccanica….

Si veda, a tal proposito, il paragrafo 2.3 del contributo del prof. Franco Ghione: ghione ottica (pdf)

Riguardo la premessa (o definizione) 7, mi avete giustamente chiesto: che vuol dire? Effettivamente Euclide lascia gli argomenti più spinosi sempre all’ultimo posto (ricordate il quinto postulato?)… Che vuol dire “cose viste sotto più raggi“? Una volta capito il concetto di grandezza apparente (misurata dall’angolo visivo che formano i contorni dell’oggetto visto con il nostro occhio) vi è evidentemente anche il concetto di nitidezza. Posso vedere una montagna e una penna sotto lo stesso angolo, e gudicarle della stessa grandezza apparente, ma certamente della penna vedrò più dettagli, e della montagna meno. Inoltre un oggetto al centro della mia visuale sarà visto più nitidamente che uno posto alla periferia del mio campo visivo.

Ciò dipende da come è fatto strutturalmente e fisiologicamente il nostro occhio. Qui un estratto sempre del contributo del prof. Ghione, qualora non l’aveste ancora scaricato……..

Nello spiegarvi che i raggi visivi (in realtà i fotoricettori della retina) del nostro occhio sono un insieme discreto, mi sono imbattuta nella profonda e fondamentale distinzione tra quantità numerabili e continue. Ma su questo importantissimo e non banale concetto potremmo fare una lezione specifica..

@@@@@@@@@@@@@@@@@@@

—>DOMANDA IMPORTANTE: AVETE TUTTI GIA’ FATTO LE PROPORZIONI IN CLASSE?<—

[rispondete nei commenti! …….ma lo leggete ‘sto blog?!?!?!]

@@@@@@@@@@@@@@@@@

La scorsa volta abbiamo rivisto meglio con Geogebra la proposizione 2, per convincerci del fatto che:

1) solo dopo averla dimostrata possiamo arbitrariamente traslare segmenti, cioè, ad esempio, “misurare un segmento col compasso” e poi riportarlo dove ci serve

2) il postulato 3 (si possono tracciare cerchi di qualsiasi centro e qualsiasi raggio) vuol dire che si può “usare un compasso” solo ed esclusivamente PRIMA puntandolo dove si vuole e POI aprendolo quanto si vuole (ma NON si può puntare un compasso DOPO averlo già aperto, o meglio lo si può fare, ma solo in virtù della proposizione 2, e non del terzo postulato!!)

Abbiamo poi iniziato l’argomento che ci porterà allo studio della prospettiva, cioè del modello matematico per rappresentare su una superficie bidimensionale, quale ad esempio un foglio, una tela o un muro, lo spazio tridimensionale “come lo vediamo”.

Ecco, appunto: “come vediamo”? (per questo “teorie della visione”)

_____________________(estratto da “Le diverse teorie della visione”, del gruppo G.A.L.S.)

Lo studio dei fenomeni luminosi  si fa risalire al periodo greco; il solo effetto conosciuto della luce era la visione, per cui la domanda che i filosofi si ponevano era: come si fa a vedere? (ricordiamo che il punto di partenza per l’indagine era  che “ogni ente fisico esisteva perché produceva degli effetti sull’uomo”)

Emissionisti (pitagorici, VI a.C.)     Dall’occhio esce un quid (tentacoli o bastoncini) che raggiunge l’oggetto visto e lo cattura: l’occhio è come una lanterna che emette “raggi visivi” (ma allora perchè ci serve la luce per vedere??)

Immissionisti (democritei, V a.C.)    La teoria atomista dei simulacri afferma che dei corpuscoli si staccano dagli oggetti per raggiungere i nostri occhi, gli oggetti mandano cioè alla nostra anima delle immagini (specie di ombre o simulacri materiali che rivestono i corpi, si agitano sulla loro
superficie e possono staccarsene, per portare alle nostre anime le forme, i colori e tutte le altre
qualità visibili).            (Lucrezio e accecamento per oggetti sfolgoranti. Accenni all’esistenza di un lumen, agente esterno necessario per provocare l’emissione dei simulacri da parte degli oggetti, in quanto questi al buio non emettono nulla che li faccia vedere, costituito da corpuscoli piccolissimi che si lanciano nello spazio e lo riempiono tutto a grandissima velocità…)      [..ricordate il discorso sulla velocità della luce? (e sul fatto che, no non si può superare!)]

Due fluidi  (empedoclei, V a.C.)      Teoria che prevede due emissioni: quella dell’occhio verso l’oggetto e quella dell’oggetto verso l’occhio. Empedocle sostiene che i due flussi sono uno esterno, esistente per sé, oggettivo, di natura corpuscolare, portante l’ordine, la forma ed il colore dell’oggetto; l’altro emesso dall’occhio per mezzo di un “fuoco” (da interpretare come spirito, anima o qualche entità ancor meno definita).

Azione tramite un mezzo (aristotelici, IV a.C.)        La teoria di Aristotele era che vi fosse un movimento che si propaga tra l’oggetto e l’occhio e che modifica lo stato dei corpi diafani. Il corpo diafano al buio è in una condizione potenziale, è diafano in potenza. Lo stesso corpo si dice che è in luce, quando è diafano in atto. La sorgente di fuoco modifica il mezzo, riusciamo a vedere perché c’è alterazione del mezzo. Se intorno all’occhio ci fosse il vuoto completo, la visione sarebbe impossibile.

__________________________________________________________

Noi, tanto per cambiare, ci occupiamo di ciò che scrisse Euclide nell’opera Ottica http://en.wikipedia.org/wiki/Euclid%27s_Optics

___________________________________________________________

Luuuunghissima digressione su via Piccolomini: ho cercato di convincervi che l’effetto ottico dato dall’avvicinarsi e vedere la cupola rimpicciolirsi è dato dal confronto (che il nostro occhio automaticamente fa) con quanto invece si ingrandiscono i palazzi che per noi sono “in primo piano” (quelli della via). Cioè i palazzi,  vicini e piccoli (rispetto alla cupola), si ingrandiscono molto mentre ci avviciniamo e a mano a mano li superiamo; la cupola invece, essendo lontana e più grande, non si ingrandisce altrettanto: ci sembra quindi rimpicciolirsi.

L’effetto (dolly zoom) di una cinepresa che si muove in avanti su un carrello, contemporaneamente zoomando indietro con l’obiettivo (o muovendosi indietro e zoomando in avanti) è ancora più strano: vedi ad esempio.

[anche qui digressione su L’odio, di Mathieu Kassovitz, che (inutile che mi chiediate di farvi vedere:è pieno di violenza, parolacce e droga) racconta, in maniera a volte dura e drammatica a volte esilarante, della vita in una banlieu parigina, e quindi di quella di un po’ tutte le borgate.. Ciò che però è il senso del film, di cui è portavoce il personaggio Hubert, è che l’odio genera altro odio, la violenza altra violenza.

Peraltro il titolo di questo blog viene proprio dall’incipit e dalla fine del film!!! XD  ]

Finalmente dotata di proiettore e computer vi ho mostrato, per curiosità, la traduzione del ‘500, ad opera del Commandino, degli Elementi di Euclide.
Dopo aver ricordato cosa s’intende per “metodo assiomatico-deduttivo” (cioè l’esistenza di un impianto logico per cui, a partire da poche affermazioni “prime”, indimostrate – le “regole del gioco” – si può arrivare a dimostrare proposizioni sempre più ariticolate riguardo gli oggetti che si sta trattando) abbiamo visto per esteso quali sono le definizioni, postulati e nozioni comuni della geometria euclidea, contenuti all’inizio del I libro degli Elementi.
__________________________________________________________

Definizioni

1. Un punto è ciò che non ha parti.
2. Una linea è una lunghezza senza larghezza.
3. Gli estremi di una linea sono punti.
4. Una retta è una linea che giace ugualmente rispetto ai punti su di essa.
5. Una superficie è ciò che ha soltanto lunghezza e larghezza.
6. Gli estremi di una superficie sono linee.
7. Una superficie piana è quella che giace ugualmente rispetto alle rette su di essa.
8. Un angolo piano è l’inclinazione reciproca di due linee in un piano le quali, si incontrino e
non giacciano in linea retta.
9. Quando le linee che comprendono l’angolo sono rette, l’angolo è detto rettilineo.
10. Quando una retta innalzata a partire da un’altra retta forma con essa angoli adiacenti
uguali fra loro, ciascuno dei due angoli è retto, e la retta si dice perpendicolare a quella su
cui è innalzata.
11. Dicesi angolo ottuso l’angolo maggiore di un angolo retto.
12. Dicesi acuto l’angolo minore di un angolo retto.
13. Dicesi termine è ciò che è estremo di qualche cosa.
14. Dicesi figura è ciò che è compreso da uno o più termini.
15. Dicesi cerchio una figura piana delimitata da un’unica linea tale che tutte le rette che
terminano su di essa a partire da un medesimo punto fra quelli interni alla figura, siano
uguali fra loro.
16. Quel punto si chiama centro del cerchio.
17. Dicesi diametro del cerchio è una retta condotta per il centro e terminata da ambedue le
parti dalla circonferenza del cerchio, la quale retta taglia anche il cerchio per metà.
18. Dicesi semicerchio è la figura compresa dal diametro e dalla circonferenza da esso
tagliata. E centro del semicerchio è quello stesso che è anche centro del cerchio.
19. Dicesi rettilinee le figure delimitate da rette, vale a dire: figure trilatere quelle comprese da
tre rette, quadrilatere quelle comprese da quattro rette e multilatere quelle comprese da
più di quattro rette.
20. Dicesi triangolo equilatero la figura trilatera che ha i tre lati uguali, triangolo isoscele quella
che ha soltanto due lati uguali, e scaleno quella che ha i tre lati disuguali.
21. Dicesi inoltre triangolo rettangolo la figura trilatera che ha un angolo retto, triangolo
ottusangolo quella che ha un angolo ottuso, e triangolo acutangolo quella che ha i tre
angoli acuti.
22. Dicesi quadrato la figura quadrilatera che ha i lati uguali e gli angoli retti.
23. Diconsi parallele rette giacenti nello stesso piano che, prolungate illimitatamente in
entrambe le direzioni, non si incontrino fra loro da nessuna delle due parti.

Postulati

Risulti postulato che
1. E’ possibile condurre una linea retta da un qualsiasi punto ad ogni altro punto.
2. E’ possibile prolungare illimitatamente una retta finita in linea retta.
3. E’ possibile descrivere un cerchio con qualsiasi centro e distanza (raggio) qualsiasi.
4. Tutti gli angoli retti sono uguali fra loro
5. Se (in un piano) una retta, intersecando due altre rette, forma con esse, da una medesima
parte, angoli interni la cui somma è minore di due angoli retti, allora queste due rette
indefinitamente prolungate finiscono con l’incontrarsi dalla parte detta.

Nozioni comuni

1. Cose uguali a un’altra medesima sono tra loro uguali.

2. Se a cose uguali si aggiungono cose uguali, allora si ottengono cose uguali.

3. Se da cose uguali si tolgono cose uguali, allora si ottengono cose uguali.

4. Cose che possono essere portate a sovrapporsi l’una con l’altra sono uguali tra loro.

5. Il tutto è maggiore della parte. ______________________________________________________

 

Il sito http://aleph0.clarku.edu/~djoyce/java/elements/bookI/bookI.html offre una versione “digitale” (e in inglese ovviamente!) degli Elementi di Euclide.

Navigando il primo libro, abbiamo visto la proposizione 2 (E’ POSSIBILE TRACCIARE UN SEGMENTO LUNGO QUANTO UN SEGMENTO DATO, A PARTIRE DA QUALSIASI PUNTO) e l’abbiamo realizzato con Geogebra.

Abbiamo rivisto quanto fatto la volta precedente: per chi era assente abbiamo ripetuto brevemente l’etimologia della parola matematica e riassunto il contenuto del brano del Menone di Platone, in cui si spiegava cosa fosse la dottrina della “reminiscenza”. Abbiamo ripetuto inoltre il teorema di Pitagora col cartoncino (questa volta magistralmente colorato!) e visto le connessioni con la formula del quadrato del binomio.

La matematica è fatta di parole o immagini? Che cos’è un simbolo?

Euclide: introduzione storica (periodo ellenistico, Museo e Biblioteca di Alessandria, sistematizzazione del sapere) e gli Elementi.

I termini greci per definizioni, postulati e assiomi

Qual’è la differenza tra postulato e teorema? Un postulato può essere “sbagliato”? (no!!) I postulati come regole del gioco: se cambio regola sto cambiando gioco

Accenni alle geometrie “non euclidee”: esse hanno postulati differenti da quelli visti; accenni alla geometria sferica.

NOTA PER TUTTI E TUTTE, COMPRESA ME: RICORDIAMOCI DI FARCI APRIRE IL COMPUTER!