@@@@@@@@@@@@@@@@@@@

—>DOMANDA IMPORTANTE: AVETE TUTTI GIA’ FATTO LE PROPORZIONI IN CLASSE?<—

[rispondete nei commenti! …….ma lo leggete ‘sto blog?!?!?!]

@@@@@@@@@@@@@@@@@

 

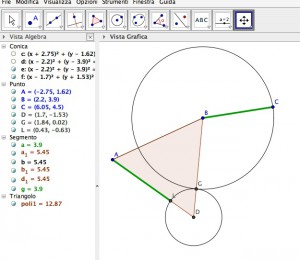
La scorsa volta abbiamo rivisto meglio con Geogebra la proposizione 2, per convincerci del fatto che:

1) solo dopo averla dimostrata possiamo arbitrariamente traslare segmenti, cioè, ad esempio, “misurare un segmento col compasso” e poi riportarlo dove ci serve

2) il postulato 3 (si possono tracciare cerchi di qualsiasi centro e qualsiasi raggio) vuol dire che si può “usare un compasso” solo ed esclusivamente PRIMA puntandolo dove si vuole e POI aprendolo quanto si vuole (ma NON si può puntare un compasso DOPO averlo già aperto, o meglio lo si può fare, ma solo in virtù della proposizione 2, e non del terzo postulato!!)

 

Abbiamo poi iniziato l’argomento che ci porterà allo studio della prospettiva, cioè del modello matematico per rappresentare su una superficie bidimensionale, quale ad esempio un foglio, una tela o un muro, lo spazio tridimensionale “come lo vediamo”.

Ecco, appunto: “come vediamo”? (per questo “teorie della visione”)

 

_____________________(estratto da “Le diverse teorie della visione”, del gruppo G.A.L.S.)

Lo studio dei fenomeni luminosi  si fa risalire al periodo greco; il solo effetto conosciuto della luce era la visione, per cui la domanda che i filosofi si ponevano era: come si fa a vedere? (ricordiamo che il punto di partenza per l’indagine era  che “ogni ente fisico esisteva perché produceva degli effetti sull’uomo”)

Emissionisti (pitagorici, VI a.C.)     Dall’occhio esce un quid (tentacoli o bastoncini) che raggiunge l’oggetto visto e lo cattura: l’occhio è come una lanterna che emette “raggi visivi” (ma allora perchè ci serve la luce per vedere??)

Immissionisti (democritei, V a.C.)    La teoria atomista dei simulacri afferma che dei corpuscoli si staccano dagli oggetti per raggiungere i nostri occhi, gli oggetti mandano cioè alla nostra anima delle immagini (specie di ombre o simulacri materiali che rivestono i corpi, si agitano sulla loro
superficie e possono staccarsene, per portare alle nostre anime le forme, i colori e tutte le altre
qualità visibili).            (Lucrezio e accecamento per oggetti sfolgoranti. Accenni all’esistenza di un lumen, agente esterno necessario per provocare l’emissione dei simulacri da parte degli oggetti, in quanto questi al buio non emettono nulla che li faccia vedere, costituito da corpuscoli piccolissimi che si lanciano nello spazio e lo riempiono tutto a grandissima velocità…)      [..ricordate il discorso sulla velocità della luce? (e sul fatto che, no non si può superare!)]

Due fluidi  (empedoclei, V a.C.)      Teoria che prevede due emissioni: quella dell’occhio verso l’oggetto e quella dell’oggetto verso l’occhio. Empedocle sostiene che i due flussi sono uno esterno, esistente per sé, oggettivo, di natura corpuscolare, portante l’ordine, la forma ed il colore dell’oggetto; l’altro emesso dall’occhio per mezzo di un “fuoco” (da interpretare come spirito, anima o qualche entità ancor meno definita).

Azione tramite un mezzo (aristotelici, IV a.C.)        La teoria di Aristotele era che vi fosse un movimento che si propaga tra l’oggetto e l’occhio e che modifica lo stato dei corpi diafani. Il corpo diafano al buio è in una condizione potenziale, è diafano in potenza. Lo stesso corpo si dice che è in luce, quando è diafano in atto. La sorgente di fuoco modifica il mezzo, riusciamo a vedere perché c’è alterazione del mezzo. Se intorno all’occhio ci fosse il vuoto completo, la visione sarebbe impossibile.

__________________________________________________________

Noi, tanto per cambiare, ci occupiamo di ciò che scrisse Euclide nell’opera Ottica http://en.wikipedia.org/wiki/Euclid%27s_Optics

___________________________________________________________

Luuuunghissima digressione su via Piccolomini: ho cercato di convincervi che l’effetto ottico dato dall’avvicinarsi e vedere la cupola rimpicciolirsi è dato dal confronto (che il nostro occhio automaticamente fa) con quanto invece si ingrandiscono i palazzi che per noi sono “in primo piano” (quelli della via). Cioè i palazzi,  vicini e piccoli (rispetto alla cupola), si ingrandiscono molto mentre ci avviciniamo e a mano a mano li superiamo; la cupola invece, essendo lontana e più grande, non si ingrandisce altrettanto: ci sembra quindi rimpicciolirsi.

L’effetto (dolly zoom) di una cinepresa che si muove in avanti su un carrello, contemporaneamente zoomando indietro con l’obiettivo (o muovendosi indietro e zoomando in avanti) è ancora più strano: vedi ad esempio.

[anche qui digressione su L’odio, di Mathieu Kassovitz, che (inutile che mi chiediate di farvi vedere:è pieno di violenza, parolacce e droga) racconta, in maniera a volte dura e drammatica a volte esilarante, della vita in una banlieu parigina, e quindi di quella di un po’ tutte le borgate.. Ciò che però è il senso del film, di cui è portavoce il personaggio Hubert, è che l’odio genera altro odio, la violenza altra violenza.

Peraltro il titolo di questo blog viene proprio dall’incipit e dalla fine del film!!! XD  ]

 

Finalmente dotata di proiettore e computer vi ho mostrato, per curiosità, la traduzione del ‘500, ad opera del Commandino, degli Elementi di Euclide.
Dopo aver ricordato cosa s’intende per “metodo assiomatico-deduttivo” (cioè l’esistenza di un impianto logico per cui, a partire da poche affermazioni “prime”, indimostrate – le “regole del gioco” – si può arrivare a dimostrare proposizioni sempre più ariticolate riguardo gli oggetti che si sta trattando) abbiamo visto per esteso quali sono le definizioni, postulati e nozioni comuni della geometria euclidea, contenuti all’inizio del I libro degli Elementi.
__________________________________________________________

Definizioni

1. Un punto è ciò che non ha parti.
2. Una linea è una lunghezza senza larghezza.
3. Gli estremi di una linea sono punti.
4. Una retta è una linea che giace ugualmente rispetto ai punti su di essa.
5. Una superficie è ciò che ha soltanto lunghezza e larghezza.
6. Gli estremi di una superficie sono linee.
7. Una superficie piana è quella che giace ugualmente rispetto alle rette su di essa.
8. Un angolo piano è l’inclinazione reciproca di due linee in un piano le quali, si incontrino e
non giacciano in linea retta.
9. Quando le linee che comprendono l’angolo sono rette, l’angolo è detto rettilineo.
10. Quando una retta innalzata a partire da un’altra retta forma con essa angoli adiacenti
uguali fra loro, ciascuno dei due angoli è retto, e la retta si dice perpendicolare a quella su
cui è innalzata.
11. Dicesi angolo ottuso l’angolo maggiore di un angolo retto.
12. Dicesi acuto l’angolo minore di un angolo retto.
13. Dicesi termine è ciò che è estremo di qualche cosa.
14. Dicesi figura è ciò che è compreso da uno o più termini.
15. Dicesi cerchio una figura piana delimitata da un’unica linea tale che tutte le rette che
terminano su di essa a partire da un medesimo punto fra quelli interni alla figura, siano
uguali fra loro.
16. Quel punto si chiama centro del cerchio.
17. Dicesi diametro del cerchio è una retta condotta per il centro e terminata da ambedue le
parti dalla circonferenza del cerchio, la quale retta taglia anche il cerchio per metà.
18. Dicesi semicerchio è la figura compresa dal diametro e dalla circonferenza da esso
tagliata. E centro del semicerchio è quello stesso che è anche centro del cerchio.
19. Dicesi rettilinee le figure delimitate da rette, vale a dire: figure trilatere quelle comprese da
tre rette, quadrilatere quelle comprese da quattro rette e multilatere quelle comprese da
più di quattro rette.
20. Dicesi triangolo equilatero la figura trilatera che ha i tre lati uguali, triangolo isoscele quella
che ha soltanto due lati uguali, e scaleno quella che ha i tre lati disuguali.
21. Dicesi inoltre triangolo rettangolo la figura trilatera che ha un angolo retto, triangolo
ottusangolo quella che ha un angolo ottuso, e triangolo acutangolo quella che ha i tre
angoli acuti.
22. Dicesi quadrato la figura quadrilatera che ha i lati uguali e gli angoli retti.
23. Diconsi parallele rette giacenti nello stesso piano che, prolungate illimitatamente in
entrambe le direzioni, non si incontrino fra loro da nessuna delle due parti.

Postulati

Risulti postulato che
1. E’ possibile condurre una linea retta da un qualsiasi punto ad ogni altro punto.
2. E’ possibile prolungare illimitatamente una retta finita in linea retta.
3. E’ possibile descrivere un cerchio con qualsiasi centro e distanza (raggio) qualsiasi.
4. Tutti gli angoli retti sono uguali fra loro
5. Se (in un piano) una retta, intersecando due altre rette, forma con esse, da una medesima
parte, angoli interni la cui somma è minore di due angoli retti, allora queste due rette
indefinitamente prolungate finiscono con l’incontrarsi dalla parte detta.

Nozioni comuni

1. Cose uguali a un’altra medesima sono tra loro uguali.

2. Se a cose uguali si aggiungono cose uguali, allora si ottengono cose uguali.

3. Se da cose uguali si tolgono cose uguali, allora si ottengono cose uguali.

4. Cose che possono essere portate a sovrapporsi l’una con l’altra sono uguali tra loro.

5. Il tutto è maggiore della parte. ______________________________________________________

 

Il sito http://aleph0.clarku.edu/~djoyce/java/elements/bookI/bookI.html offre una versione “digitale” (e in inglese ovviamente!) degli Elementi di Euclide.

Navigando il primo libro, abbiamo visto la proposizione 2 (E’ POSSIBILE TRACCIARE UN SEGMENTO LUNGO QUANTO UN SEGMENTO DATO, A PARTIRE DA QUALSIASI PUNTO) e l’abbiamo realizzato con Geogebra.

Abbiamo rivisto quanto fatto la volta precedente: per chi era assente abbiamo ripetuto brevemente l’etimologia della parola matematica e riassunto il contenuto del brano del Menone di Platone, in cui si spiegava cosa fosse la dottrina della “reminiscenza”. Abbiamo ripetuto inoltre il teorema di Pitagora col cartoncino (questa volta magistralmente colorato!) e visto le connessioni con la formula del quadrato del binomio.

La matematica è fatta di parole o immagini? Che cos’è un simbolo?

Euclide: introduzione storica (periodo ellenistico, Museo e Biblioteca di Alessandria, sistematizzazione del sapere) e gli Elementi.

I termini greci per definizioni, postulati e assiomi

Qual’è la differenza tra postulato e teorema? Un postulato può essere “sbagliato”? (no!!) I postulati come regole del gioco: se cambio regola sto cambiando gioco

Accenni alle geometrie “non euclidee”: esse hanno postulati differenti da quelli visti; accenni alla geometria sferica.

 

 

NOTA PER TUTTI E TUTTE, COMPRESA ME: RICORDIAMOCI DI FARCI APRIRE IL COMPUTER!

• Che cos’è la matematica? A cosa serve?
• Etimologia della parola (la divinità egizia Maat e il verbo greco manthàno)
• Accenni al platonismo e lettura di un estratto del Menone
• Il teorema di Pitagora dimostrato col cartoncino

[….noblogs non mi fa caricare le slides!!!!!!!]

Dal sito di Maddmaths (http://maddmaths.simai.eu/maddcosa/)
“La matematica è un po’ la bestia nera di tutti gli studenti e non ha una buona reputazione presso il cittadino medio, nonostante gli sforzi, spesso eroici, di alcuni insegnanti validi e preparati che cercano di presentare questa materia in un modo più vivo e attraente. Certo, ci sono stati libri e film e spettacoli teatrali che hanno cercato di raccontarcela un po’ meglio, ma spesso l’immagine che ne risulta è più vicina a quella del matematico pazzo o a quella dello scienziato brillante con idee spesso fantasiose. Alla fine, la realtà è è probabilmente in un qualche punto intermedio fra queste due posizioni (…).
(…) Oggi i matematici si occupano di ottimizzazione di processi industriali, di traffico veicolare e pedonale, della gestione delle reti di dati, del trattamento e compressione di immagini, della criptografia su web e nelle banche. Sono coinvolti nelle previsioni meteorologiche, nel disegno di reti idriche, nella prevenzione di catastrofi naturali. Sono alle frontiere della genomica e della proteomica e risultano indispensabili per la progettazione di videogiochi ed effetti speciali al cinema. Sono dietro agli algoritmi che gestiscono i vari motori di ricerca su web, Google fra tutti. Insomma, in Italia, ma ancora di più all’estero, la professione del matematico occupa spazi sempre maggiori ma di questi successi, e dei possibili sviluppi, si parla poco e di solito in modo poco informato.”

 

Etimologia del termine

Da Wikipedia:
(…) l’origine del termine proviene dal vocabolo egizio maat, nella cui composizione appare il simbolo del cubito, strumento di misura lineare: un primo accostamento al concetto matematico. Simbolo geometrico di questo ordine è un rettangolo, da cui sorge la testa piumata della dea egizia Maat, personificazione dei concetti di ordine, verità e giustizia, figlia di Ra, unico Uno, creatore di ogni cosa, ma neppure il padre può vivere senza la figlia: la sua potenza demiurgica è limitata e ordinata da leggi matematiche. All’inizio del papiro Rhind si trova questa affermazione: “Il calcolo accurato è la porta d’accesso alla conoscenza di tutte le cose e agli oscuri misteri”.

 

 

 

Il verbo manthàno da cui deriva (il plurale neutro) tà mathematikà: “le cose che possono essere apprese”. Il platonismo e la dottrina delle idee. Lettura di un estratto del Menone e il teorema di Pitagora dimostrato “visivamente”.

 

Programma progetto IFA matematica Liceo Dante

• Introduzione
  

Che cos’è la matematica secondo i ragazzi? A cosa serve?

Etimologia della parola dal greco: ciò che può essere appreso, ma manthàno ha in sé anche il concetto di una divinità che rivela (dea egiziana Maat della piuma); accenni al platonismo, di cui vedremo struttura e significato del 5 solidi; lettura di un estratto del Menone.

• La geometria euclidea
  

La matematica è una disciplina astratta, che si fonda sulle parole, o concreta, fatta da immagini? Il carattere eminentemente geometrico della matematica greca classica: il teorema di Pitagora dimostrato “visivamente” (col cartoncino).

Struttura della matematica: definizioni, assiomi, postulati, teoremi.

Gli Elementi di Euclide: hòroi, aitèmata, koinài ennòiai; i postulati come richieste (non ha senso domandarsi se siano veri o falsi, se li cambio, sto cambiando geometria).

L’esempio di una formica che vive su una sfera: lei chiama “rette” quelle che noi chiamiamo “cerchi” (accenni alle geometrie non euclidee).

Introduzione a Geogebra: si ripercorre quanto visto attraverso l’utilizzo di un software di geometria dinamica. Qualche proposizione con Geogebra: esempio interessante la proposizione 2: da non confondere cl terzo postulato!

• La geometria della visione e la prospettiva
  

L’Ottica di Euclide come primo testo scientifico sulla geometria della visione (considerazioni storiche e scientifiche, senza approfondire eccessivamente la geometria su cui si basa; se vi sono i prerequisiti sulla similitudine e la congruenza si può vedere qualche semplice teorema)

La prospettiva nella pittura: dalla stanza delle maschere (casa di Augusto, I sec a.C.) a Piero della Francesca (De prospectiva pingendi, 1482): attraverso le immagini  si fa un viaggio nella storia dell’arte, osservando come la “corretta” impostazione prospettica di un dipinto si basa su una schematizzazione rigorosa della superficie (bidimensionale) su cui si ritrae una realtà tridimensionale.

 La galleria prospettica di Palazzo Spada: visita (2h)

Il concetto di dimensione attraverso Flatlandia (proiezione integrale o di spezzoni significativi); e noi abitanti delle tre dimensioni, come possiamo “vedere” la quarta? L’Ipercubo di Pierelli, la grafica di Todesco (Hypersphere).

• Il concetto di simmetria.
  

[Che cos’è un angolo? I poligoni regolari e le loro proprietà.] E se il numero dei lati diventasse infinitamente grande (e la loro lunghezza infinitamente piccola)?[Che cos’è un diedro? I poliedri regolari e i poliedri troncati.]

Mattonelle, tassellazioni e fregi: ricoprire superfici con poligoni. L’arte di Escher e le tassellazioni non periodiche di Penrose. Le stuoie africane.

I cristalli di neve e il dna (le simmetrie esagonali).

Le simmetrie in architettura

• Musica, Logica, Grafica: l’eterna ghirlanda brillante (di Goedel, Escher, Bach)

Canoni eternamente ascendenti e scale infinite.

Si è già visto come nell’arte si siano sfruttate spesso costruzioni matematiche per descrivere meglio la realtà, vediamo ora come invece la matematica si possa sfruttare per ottenere effetti sorprendenti. Escher e lo spazio: il nastro di Moebius come semplice costruzione di superficie non orientata (da fare con la striscia di carta); la ricerca dell’infinito e le figure impossibili.

Logica: nozioni di base e accenni al teorema di Goedel         (–>Smullyan)

• Sezione aurea, numeri di Fibonacci, spirali, fillotassi, broccoli e frattali
  

Rettangolo e rapporto aureo in arte e in matematica.

Spirale logaritmica

Ancora solidi platonici

Successione (di Fibonacci e ancora spirali)

Brainstorming sul broccolo: che proprietà ha? Guardata nella sua interezza e con una lente di ingrandimento, cosa possiamo dire della sua forma?

Il frattale come immagine dotata di omotetia interna o autosimilarità. Soprassedendo sulla definizione matematica che impiega numeri complessi e il concetto di sistema dinamico, costruiamo a mano la curva di Koch (frattale lineare).