Finalmente dotata di proiettore e computer vi ho mostrato, per curiosità, la traduzione del ‘500, ad opera del Commandino, degli Elementi di Euclide.
Dopo aver ricordato cosa s’intende per “metodo assiomatico-deduttivo” (cioè l’esistenza di un impianto logico per cui, a partire da poche affermazioni “prime”, indimostrate – le “regole del gioco” – si può arrivare a dimostrare proposizioni sempre più ariticolate riguardo gli oggetti che si sta trattando) abbiamo visto per esteso quali sono le definizioni, postulati e nozioni comuni della geometria euclidea, contenuti all’inizio del I libro degli Elementi.
__________________________________________________________

Definizioni

1. Un punto è ciò che non ha parti.
2. Una linea è una lunghezza senza larghezza.
3. Gli estremi di una linea sono punti.
4. Una retta è una linea che giace ugualmente rispetto ai punti su di essa.
5. Una superficie è ciò che ha soltanto lunghezza e larghezza.
6. Gli estremi di una superficie sono linee.
7. Una superficie piana è quella che giace ugualmente rispetto alle rette su di essa.
8. Un angolo piano è l’inclinazione reciproca di due linee in un piano le quali, si incontrino e
non giacciano in linea retta.
9. Quando le linee che comprendono l’angolo sono rette, l’angolo è detto rettilineo.
10. Quando una retta innalzata a partire da un’altra retta forma con essa angoli adiacenti
uguali fra loro, ciascuno dei due angoli è retto, e la retta si dice perpendicolare a quella su
cui è innalzata.
11. Dicesi angolo ottuso l’angolo maggiore di un angolo retto.
12. Dicesi acuto l’angolo minore di un angolo retto.
13. Dicesi termine è ciò che è estremo di qualche cosa.
14. Dicesi figura è ciò che è compreso da uno o più termini.
15. Dicesi cerchio una figura piana delimitata da un’unica linea tale che tutte le rette che
terminano su di essa a partire da un medesimo punto fra quelli interni alla figura, siano
uguali fra loro.
16. Quel punto si chiama centro del cerchio.
17. Dicesi diametro del cerchio è una retta condotta per il centro e terminata da ambedue le
parti dalla circonferenza del cerchio, la quale retta taglia anche il cerchio per metà.
18. Dicesi semicerchio è la figura compresa dal diametro e dalla circonferenza da esso
tagliata. E centro del semicerchio è quello stesso che è anche centro del cerchio.
19. Dicesi rettilinee le figure delimitate da rette, vale a dire: figure trilatere quelle comprese da
tre rette, quadrilatere quelle comprese da quattro rette e multilatere quelle comprese da
più di quattro rette.
20. Dicesi triangolo equilatero la figura trilatera che ha i tre lati uguali, triangolo isoscele quella
che ha soltanto due lati uguali, e scaleno quella che ha i tre lati disuguali.
21. Dicesi inoltre triangolo rettangolo la figura trilatera che ha un angolo retto, triangolo
ottusangolo quella che ha un angolo ottuso, e triangolo acutangolo quella che ha i tre
angoli acuti.
22. Dicesi quadrato la figura quadrilatera che ha i lati uguali e gli angoli retti.
23. Diconsi parallele rette giacenti nello stesso piano che, prolungate illimitatamente in
entrambe le direzioni, non si incontrino fra loro da nessuna delle due parti.

Postulati

Risulti postulato che
1. E’ possibile condurre una linea retta da un qualsiasi punto ad ogni altro punto.
2. E’ possibile prolungare illimitatamente una retta finita in linea retta.
3. E’ possibile descrivere un cerchio con qualsiasi centro e distanza (raggio) qualsiasi.
4. Tutti gli angoli retti sono uguali fra loro
5. Se (in un piano) una retta, intersecando due altre rette, forma con esse, da una medesima
parte, angoli interni la cui somma è minore di due angoli retti, allora queste due rette
indefinitamente prolungate finiscono con l’incontrarsi dalla parte detta.

Nozioni comuni

1. Cose uguali a un’altra medesima sono tra loro uguali.

2. Se a cose uguali si aggiungono cose uguali, allora si ottengono cose uguali.

3. Se da cose uguali si tolgono cose uguali, allora si ottengono cose uguali.

4. Cose che possono essere portate a sovrapporsi l’una con l’altra sono uguali tra loro.

5. Il tutto è maggiore della parte. ______________________________________________________

 

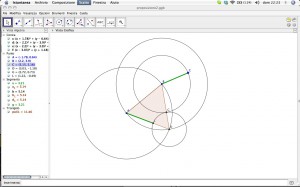
Il sito http://aleph0.clarku.edu/~djoyce/java/elements/bookI/bookI.html offre una versione “digitale” (e in inglese ovviamente!) degli Elementi di Euclide.

Navigando il primo libro, abbiamo visto la proposizione 2 (E’ POSSIBILE TRACCIARE UN SEGMENTO LUNGO QUANTO UN SEGMENTO DATO, A PARTIRE DA QUALSIASI PUNTO) e l’abbiamo realizzato con Geogebra.