Proseguiamo lo studio delle simmetrie in arte parlando di (e ascoltando, ovviamente!) musica.

Nello specifico leggiamo l’articolo di Benedetto Scimemi, Contrappunto musicale, (in Matematica e Cultura 2001, a cura di M. Emmer, Springer, 2001).

Utilizzeremo le simmetrie piane (di cui abbiamo già parlato), cioè:

• traslazioni
• riflessioni
• rotazioni

Prendiamo lo spartito di fra’ Martino e applichiamo una riflessione orizzontale (nell’articolo riflessione lago) rispetto, ad esempio, al terzo rigo del pentagramma (quindi i punti fissi saranno tutti i “si”). Il ritmo sarà lo stesso, ma la melodia completamente diversa: la “tristezza” è data dal modo minore.

Ora applichiamo una riflessione orizzontale (nell’articolo riflessione muro) sullo spartito originario: leggiamolo cioè all’indietro:

Ora prendiamo lo spartito ed effettuiamo una rotazione di mezzo giro o, equivalentemente applichiamo una riflessione orizzontale e poi una verticale, o viceversa… infatti possiamo pensare un pentagramma come un rettangolo sufficientemente lungo: le simmetrie prese in considerazione possono cioè essere composte, in quanto formano un gruppo (diedrale D_4, o di Klein).

Ora che abbiamo capito come “agiscano” queste simmetrie sugli spartiti, vediamo come Bach le utilizzi per le diverse variazioni (Goldberg, ad esempio).

Dopo aver visto l’utilizzo delle simmetrie in architettura, vediamo oggi come esse si presentino in natura, con le strutture reticolari dei cristalli: in particolare ci interesserà la forma (e le possibili simmetrie, dunque) del cristallo di neve.

Probabilmente vi è stato detto già alle medie, che ciò che vediamo macroscopicamente in un cristallo, rispecchia ciò che avviene a livello molecolare, cioè la forma (microscopica) che assumono gli atomi nel formare appunto la molecola.

Un esempio che tutti avete presente è il cloruro di sodio (anche detto sale! eh sì, è un cristallo anche lui..) che forma dei grani (cristalli) cubici,

in quanto gli atomi di cloro e di sodio formano la molecola di sale in questo modo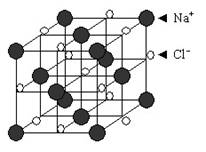    

I cristalli di neve invece hanno una struttura esagonale, dovuta appunto alla disposizione delle molecole di H2O

(su questo sito del California Insitute of Technology vi sono tutte le informazioni scientifiche, foto al microscopio e quant’altro voi possiate desiderare di sapere sui cristalli di neve!! http://www.its.caltech.edu/~atomic/snowcrystals/)

Alcune foto al microscopio di alcuni tipi di fiocchi di neve

I cristalli di neve disegnati da Cartesio

Vedremo inoltre cosa queste simmetrie esagonali del ghiaccio abbiano in comune col DNA..

[Su questo sito invece trovate molto materiale su cosa siano i gruppi di simmetria dello spazio tridimensionale, compreso un software che vi permette di visualizzarli!! http://www.spacegroup.info/html/space_groups.html.]

Trovo che il metodo “vi do la definizione, poi vediamo le proprietà, e poi gli esempi e/o le applicazioni” renda la matematica a volte noiosa.. stavolta proviamo a fare il percorso inverso, vediamo prima come vengano sfruttate le simmetrie, in particolare, in architettura.

[In realtà a grandi linee, con l’esempio del rettangolo, abbiamo già visto che cosa sia una simmetria di una figura; nel caso specifico del rettangolo abbiamo trovato tre elementi (più uno banale, detto identità, che è quello che non muove il rettangolo)  che sono movimenti rigidi che non alterano la forma del rettangolo, che lo “mandano in sè stesso” , e che possono essere “composti” (nel senso di: applicati uno dopo l’altro) e il risultato di tale composizione è un altro elemento del gruppo (compresa la trasformazone banale). Vi ho detto che quest’oggetto fatto di quattro elementi e di una tabella delle composizioni, è detto gruppo di Klein (in realtà gruppo diedrale D_4… ma non c’è ambiguità poichè sono isomorfi, che dal greco vuol dire….)]

Leggiamo quindi l’articolo di Kim Williams “Le simmetrie in architettura” in Matematica e Cultura 2001, a cura di M. Emmer, Springer, 2001.

La simmetria come concetto “unificante”: cos’hanno in comune i seguenti edifici?

La secentesca Rundetårn di Copenhagen e la Torre Pendente di Pisa

L’Astrodome di Houston e la cupola del Pantheon

Vediamo i diversi tipi di simmetria (che talvolta possono essere combinati insieme: ciò che la Williams nell’articolo chiama “simmetrie multiple”) in architettura e che effetto abbiano sullo spettatore li che vede/attraversa/”vive”.

SIMMETRIE BILATERALI (O ASSIALI)

Facciata del Pantheon

Alamo Sant’Antonio in Texas

Praça do Comercio a Lisbona

DUALISMO

Oratorio di Orsanmichele a Firenze

ROTAZIONI E RIFLESSIONI

Sacrestia S. Spirito a Firenze

(non trovo l’immagine!!)

Cupola del Brunelleschi di S. Maria del Fiore a Firenze

SIMILARITA’

Opera House di Sidney

Castel del Monte, Puglia

SIMMETRIA A SPIRALE O ELICOIDALE

Torciglione Vor Frelsers Kirke, Copenhagen

Cupola S. Ivo alla Sapienza

Museo Guggenheim di New York

SIMMETRIE ROTAZIONE+RIFLESSIONE+SIMILARITA’

Pavimentazione S. Maria del Fiore, Firenze

(quasi tutte le immagini sono prese da Wikipedia)

Scusate la latitanza della scorsa settimana, sapete il perchè..

Abbiamo letto “La quarta dimensione (euclidea): matematica e arte” di Michele Emmer (in Matematica e Cultura 2001, a cura di M. Emmer, Springer, 2001)

L’articolo di Emmer inizia con una citazione di U. Bottazzini, “La scienza dello spazio e la geometria immaginaria”  (in Il flauto di Hilbert, UTET, 2003) sulle lettere tra Gauss e Bolyai che tentavano di dimostrare il V postulato.. ma noi sappiamo che non è possibile!  (aveva ragione il padre di Jànos Bolyai, Farkas….) quindi Bolyai ha scoperto/inventato/deciso/postulato? una nuova geometria, quella iperbolica.

Riemann e il concetto di varietà, nel tentativo di una visione globale della geometria come studio di spazi di qualsiasi dimensione e “tipo”.

Il programma di Erlangen, Klein, la bottiglia e il gruppo (di simmetrie del rettangolo): costruzione “a mano” della tabella delle composizioni dei suoi 4 elementi.

Poincaré osserva che come si possono immaginare geometrie non euclidee, così si possano anche pensare mondi a quattro (o più) dimensioni..

Abbiamo visto la prima e l’ultima parte di Flatlandia e poi parlato di cubismo, ipercubi e ipersfere 1 e 2